《高尔顿板是正态分布?NO。近似罢了》
《高尔顿板是正态分布?NO。近似罢了》
阿睿睿《高尔顿板是正态分布?NO。近似罢了》
作者:阿睿睿
一颗小球从高尔顿板顶端落下,每遇到一个钉子,就有一半概率向左、一半概率向右。经过多层后,小球在底部的槽中堆成了一个漂亮的钟形。我们常常说:
“看,这就是正态分布!”
但,真的是吗?——并不完全。
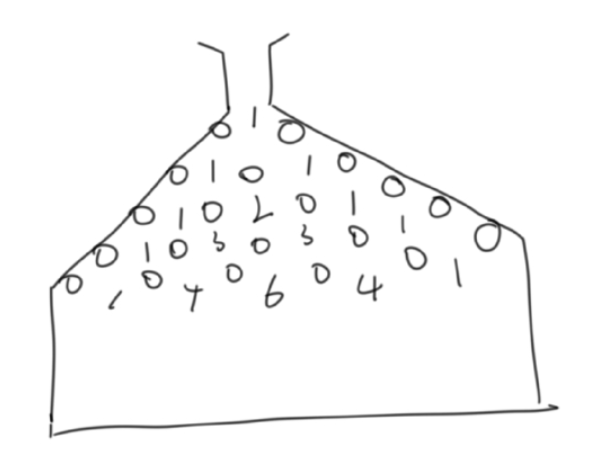
咦?仔细看那张高尔顿板的图,钉子上居然标了数字。这些数字不是随便写上去的——它们恰好组成了我们熟悉的杨辉三角。
从顶端落下一颗小球,每遇到一个钉子,它都有两种选择:向左或者向右。如果我们在每个钉子的位置,数一数“有多少条不同的路径能到这里”,结果就正好是杨辉三角的每一个数字。
第一层,只有 1 条路径(当然);
第二层,左右各 1 条;
第三层,中间的钉子可以从左上或右上两条路径到达,所以是 2;
再往下,路径数依次变成 1、3、3、1……——这不就是杨辉三角的行列式样吗?
换句话说,高尔顿板上每个钉子下方的数字,其实是一个组合数:
表示从上到第 (n) 层、第 (m) 个位置(从左数)的小球,可能有多少条路径到达这里。
而因为每次左右选择的概率相等,一颗球最终落在底部第 (m) 个槽中的概率,就是该位置路径数除以所有路径总数:
这正是著名的 二项分布(Binomial Distribution) 的形式:
高尔顿板,原来是一个「物理化的杨辉三角」;
而杨辉三角,则是二项分布的几何化表达。
前面我们看到,高尔顿板底部第 (m) 个槽的小球概率,可以用二项分布表示:
为什么这个离散分布看起来像正态分布呢?关键在于二项分布本质上是独立伯努利试验之和。
设每层落球的结果为伯努利随机变量 (Y_i):
那么小球最终落在底部的总位置可以表示为这些伯努利变量的和:
这正是二项分布的定义。
根据中心极限定理(Central Limit Theorem, CLT),当试验次数 (n-1) 很大时,独立随机变量的和经过标准化后会逼近标准正态分布:
因此,二项分布可以用正态分布近似:
这就是为什么高尔顿板底部小球堆积的分布,看起来像钟形曲线——
它并非天然正态,而是大量独立随机事件累积的极限形态。
哎呀,实际中不可能每次碰钉子都是左右概率完全相等的吧?可能因为摩擦、轻微偏斜或者钉子排列不完美,向左和向右的概率 (p) 和 (1-p) 会略有不同。
如果向右概率为 (p ≤ 0.5),每次伯努利试验仍然可以表示为:
小球最终位置仍然是这些独立试验的和:
分布不再对称,会出现轻微偏斜,其偏度(skewness)为:
随着层数 (n) 增大,偏度逐渐减小,因此即使左右概率不一样,大量独立随机事件累加的结果仍然会近似正态分布:
所以,高尔顿板即使轻微倾斜或者左右概率不完全相等,最终落球分布仍呈钟形,只是会偏向概率较大的一边。